Lei de Benford: as eleições foram fraudadas?

Muito se tem discutido sobre fraudes nas eleições, debate que ressurge em intervalos periódicos no cenário nacional. No ano de 2018, às vésperas da votação, viralizou um vídeo da produtora Brasil Paralelo, “estrelando” o senhor Hugo César Hoeschl, falando que as eleições de 2014 foram fraudadas e que as de 2018 também seriam.

Será que isso é verdade?

Para começar, quem é o senhor Hugo César Hoeschl?

Ele é um ex-procurador de carreira da Fazenda Nacional, que foi exonerado do cargo, tendo respondido a vários processos administrativos e criminais por desvios quando atuava no cargo. O procurador também foi investigado criminalmente por fraudes à licitação[1].

Em 2018, no referido vídeo, esse senhor que alardeou que houve 73,14% de probabilidade das eleições de 2014, vencidas por Dilma Rousseff contra o então candidato Aécio Neves, terem sido manipuladas.

Mas, afinal, com base em que ele afirma que houve fraude?

Bem, basicamente, ele faz um apelo à ignorância e à autoridade, quando fala na chamada Lei de Benford, sem explicar o que é essa lei e qual sua relação com as eleições, com a certeza de que o público não irá atrás de se informar sobre o que significa a lei.

Compreendendo a Lei de Benford

Para facilitar a compreensão, vamos utilizar um exemplo, qual seja, o número de habitantes nos municípios brasileiros. Conforme estatísticas oficiais[1], São Paulo tem cerca de 12 milhões e 300 mil pessoas, o Rio de Janeiro tem umas 6 milhões e setecentas mil e Salvador tem quase 3 milhões. Ou seja, o número de habitantes da cidade de São Paulo se inicia com o algarismo 1; do Rio de Janeiro se inicia com o algarismo 6; de Salvador, com o algarismo 2 e assim por diante. Se fosse para chutarmos, qual seria o primeiro algarismo do número de habitantes da maioria dos municípios brasileiros? Ou, pensando de maneira mais genérica e audaciosa, se extraíssemos todos os primeiros dígitos de todos os municípios, será que haveria algum padrão nesta distribuição?

Uma resposta “intuitiva” é a de que provavelmente haveria tantos municípios com números iniciais 1, quanto com números 2 ou 9. Mas a Lei de Benford nos diz justamente o contrário: haveria mais ou menos 30% dos municípios cuja população começa com o número 1, seguidos de 17% de números 2; 12% de números 3, decaindo até mais ou menos 5% de números 9.

De modo que podemos resumir a lei de Benford-Newcomb ou lei dos primeiros dígitos, da seguinte forma: em estatísticas aleatórias (como o número de habitantes de cidades no país, ou valores de transferências bancárias de um banco), o número 1 deve aparecer mais vezes como o primeiro algarismo, o número 2, deve aparecer mais vezes que o número 3, é assim por diante, conforme uma porcentagem pré-definida.

E o interessante é que isso ocorre nas mais diversas estatísticas do mundo real.

Exemplo de caso prático de aplicação da Lei de Benford

Para entendermos, vamos pegar um exemplo real: quanto à covid-19, qual é o primeiro algarismo que mais aparece no número de casos dos municípios brasileiros? A resposta é o número 1. Em setembro de 2020, dos 5565 municípios brasileiros, em 1.557 localidades, o algarismo 1 era o primeiro dígito do número do total de contaminações, o que corresponde a 28% dos municípios[2]. O segundo número mais recorrente é o 2, associado a 960 municípios, ou 17%. Em terceiro, o 3, com 756 locais. E assim sucessivamente, até o algarismo 9.

Por que essa lei existe?

Compreendido como a lei funciona, precisamos nos perguntar: por que isso acontece?

Bem, vamos imaginar um município brasileiro com 1.000 habitantes, nosso primeiro dígito seria 1. Para ter essa população com um primeiro dígito 2, ela deverá crescer para 2.000, e ir de 1.000 para 2.000 significa um aumento de 100%. Digamos que a população cresça a taxa média de 20% ao ano. Significa que levaria quatro anos para ir de 1 para 2 como primeiro dígito. Mas suponhamos que a população desse mesmo município seja de 5000 habitantes, o que vai requerem apenas um aumento de 20% para alcançarmos os 6.000 habitantes e mudar o primeiro dígito, e isso seria alcançado em apenas um ano (muito menos tempo). Quando a população alcança 9.000 habitantes, leva apenas um aumento de 11% e apenas sete meses para alcançar a marca de 10.000 habitantes, no qual inicia com o número 1. A partir deste ponto, o ciclo se inicia novamente com o primeiro dígito 1.

Em outras palavras, o número 1 predomina em cada passo da progressão, pois isso ocorre em sequência logarítmica. Para simplificar ainda mais: para quem ganha 1000 reais, é muito mais difícil ganhar um aumento para 2000 do que quem ganha 9000 reais passar a ganhar 10 mil. Isso vale para populações de cidades e número de páginas de livros.

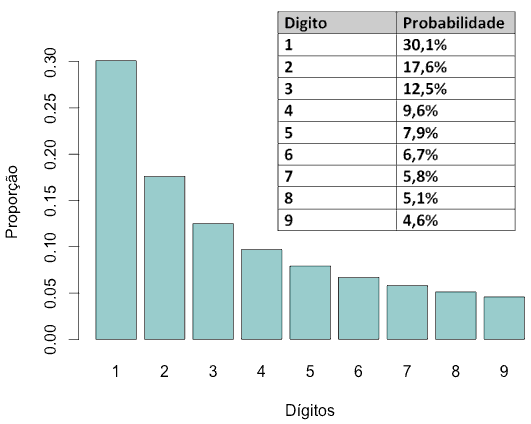
Em resumo, se pegarmos estatísticas aleatórias, como os casos de covid-19 em municípios brasileiros, é esperado que 30,1% dos municípios tenham o número de casos começando com 1; 17,6% começando com 2 e assim por diante, conforme esse gráfico.

Importância da Lei de Benford

A importância prática é justamente para detectar indícios de fraudes, já que essa lei descreve algo que é constatado naturalmente. Se os números de casos de covid dos municípios estivessem sendo fraudados, a Iei de Benford poderia ser um indício dessa fraude; se alguém alterar artificialmente os números de depósitos de um banco, ou dados contábeis, esses novos números provavelmente vão destoar do que era esperado pela Lei de Benford.

Aliás, quanto à covid-19, a Lei de Benford tem sido aplicada para confirmar os dados da China, já que muita gente desconfia dos números chineses de casos, mas um estudo de pesquisadores da Universidade de Oxford, aplicando a teoria, mostrou que a pandemia se comportou no país como na Itália e em território americano, resultado que pode desapontar os teóricos da conspiração.

Lei de Benford e eleições brasileiras

Bem, assim como os casos de covid que a gente mencionou, a população dos municípios brasileiros é bem ajustada à Lei de Benford. Assim como o número de eleitores de cada município e, por consequência o número de votantes. Então, era de se esperar que o número de votos de cada candidato à presidência, em cada município, fosse também bem ajustado à lei. Mas, surpreendentemente, não foi.

Só que, antes de explicarmos isso, para entendermos o que aconteceu, algumas considerações são necessárias.

Limitações da Lei de Benford

É importante destacar que a Lei de Benford pode dar indícios de fraude, mas não é uma prova cabal. Primeiro porque os dados da vida real se aproximam da Lei de Benford, mas não são exatamente iguais; e segundo porque a realidade pode sim ser diferente do que seria esperado pela Lei, especialmente se a amostragem não for grande o suficiente.

Aí, temos um detalhe importantíssimo: essa lei só funciona se estivermos olhando alguma estatística que tenha várias ordens de grandeza (centenas, milhares etc.). Se estivermos falando do número de páginas de livros de uma biblioteca, por exemplo, é bem provável que essa lei falhe, porque livros, em geral, tem poucas centenas de livros até, no máximo, 1 ou 2 mil páginas. Se estivermos falando da idade da população, novamente, a lei vai falhar, já que a idade das pessoas não tem várias ordens de grandeza, chegando, ao máximo e muito raramente, na casa das centenas.

Bem, então, existiu ou não fraude nas votações?

Como indicado, aí é que está o grande problema de usar essa lei para afirmar que houve fraudes nas eleições. Especificamente no caso do Brasil, conforme explica Carlos Cinelli[3], apesar de a distribuição do número de eleitores (ou da população) por municípios ter um bom ajuste com a lei de Benford quando usamos os dados do Brasil inteiro, isso não precisa valer para cada estado separadamente. E de fato não vale. Quanto ao número de habitantes de cada um dos municípios baianos, por exemplo, é bem discrepante do que se esperaria pela lei de Benford, o que vale também para Minas Gerais, Pernambuco, Piauí e Rio Grande do Sul, que foram justamente estados nos quais a lei indicaria que houve algum tipo de fraude.

Joseph Deckert e outros vão além, ao afirmar que,

“olhando dados de Ohio, Massachusetts e Ucrânia, bem como dados gerados artificialmente por uma série de simulações, a Lei de Benford se mostra essencialmente inútil como um indicador de fraude eleitoral. Podem surgir desvios com o primeiro ou segundo dígitos, mesmo em eleições livres e justas. Na verdade, uma tentativa elaborada de fraude poderia justamente tentar encaixar os dados à lei, podendo ocasionar, portanto, conclusões totalmente errôneas”[4].

Conclusão

Como escreve Carlos Cinelli, a lei de Benford nunca valerá exatamente, será apenas uma aproximação, sendo que testes estatísticos formais tem que ser interpretados com cautela, de modo que a principal função da lei de Benford é identificar possíveis focos de observações que mereçam análise/auditoria mais aprofundada.

Enfim, essa lei não diz nada sobre fraudes eleitorais no Brasil.

REFERÊNCIAS

[1] https://www.conjur.com.br/2015-mai-06/mpf-rejeita-denuncia-expoe-farsa-procurador-fazenda

[2] DANA, Samy. Teoria do 1º número explica desde as populações até a covid-19. Disponível em https://jovempan.com.br/opiniao-jovem-pan/comentaristas/samy-dana/teoria-do-1o-numero-explica-desde-as-populacoes-ate-a-covid-19.html. Acesso em maio de 2021.

[3] CINELLI, Carlos. Indício de fraude nas eleições? Usando a Lei de Benford. Disponível em https://analisereal.com/2014/11/02/indicio-de-fraude-nas-eleicoes-usando-a-lei-de-benford/. Acesso em maio de 2021.

^[4] DECKERT, J.; MYAGKOV, M.; ORDESHOOK, P.C. The Irrelevance of Benford’s Law for Detecting Fraud in Elections. Disponível em http://web.archive.org/web/20140517120934/http://vote.caltech.edu/sites/default/files/benford_pdf_4b97cc5b5b.pdf. Acesso em maio de 2021